Resolution Tests
Variation Measurement for 50mm SLR Lenses
Last week we posted an introductory article on how we measure copy-to-copy variation in different lenses. I’ll be continuing to publish these results over the next few weeks for prime lenses. We will eventually have a database put up, but I think it’s important to look at the different lenses in smaller groups, illustrating some principles that contribute to variation. It’s far too easy (and comfortable) to just believe quality control is the answer to variation. There’s a lot more to it than just quality control and I think this series of posts will help illustrate that.
We got a lot of good suggestions about our methods after the first post, considered all of it, and tried out some of it (particularly formula and graphing adjustments). We didn’t make any changes to our mathematical formula, but are going to change terminology just a bit. JulianH and several others pointed out that using the term ‘variation number’ was counter-intuitive; our numerical score gets higher when the lens has less copy-to-copy variation. It makes more sense to call it a ‘consistency score’, because a higher number means the lens is more consistent (it has less copy-to-copy variation). So from now on, the numerical score will be referred to as the Consistency Score.

- Copyright Lensrentals.com, 2015
Today we’ll take a look at the 50mm wide-aperture prime lenses and compare them to the 24mm prime lenses we posted last week. This should be an interesting comparison for several reasons. The 24mm lenses are all retrofocus designs containing 10 to 12 lens groups and at least 1 aspheric element. The ones we tested were all of fairly recent design, having been released after 2008. A 24mm f/1.4 is just about the most extreme combination of wide-angle and wide-aperture anyone currently makes (an exception being the Leica 21mm f/1.4). We thought that 50mm lenses, being mostly of simpler design, might show more consistency (less copy-to-copy variation).
The 50mm lenses are mostly double Gauss designs containing 5 to 7 elements. There are two exceptions, though. The Sigma 50mm f/1.4 Art lens and the Zeiss 55mm f/1.4 Otus are both more complex, retrofocus designs with the Sigma containing 8 groups and the Otus – 10. Most have no aspheric elements, although there are a couple of exceptions: the Sigma Art and Canon 50mm f/1.2 L have a single aspheric element, while the Zeiss Otus has a double-sided aspheric element. We also have a nice range of design dates, with the Canon 50mm f/1.4 released in 1993, several of these lenses released around 2004-2006, and a handful released just in the last year or two. Plus the 50mm lenses have a price range from under $200 to nearly $4000. It will be interesting to see if any of these factors seem to affect variation.
MTF Curves of the 50mm Lenses
Ten copies of each lens were tested on our Trioptics Imagemaster Optical Bench using the standard protocol, which we described in the last blog post. All lenses are tested at their widest apertures, so take that into consideration when comparing MTFs; stopping an f/1.4 or f/1.2 lens down to f/1.8 would improve it’s MTF. (And yes, I realize how nice it would be to have done the 50mm f/1.2 at f/1.4 and all the lenses at f/1.8. I might get to it someday. Maybe.)
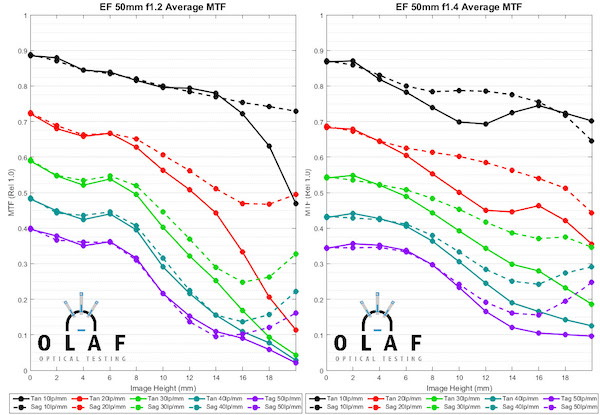
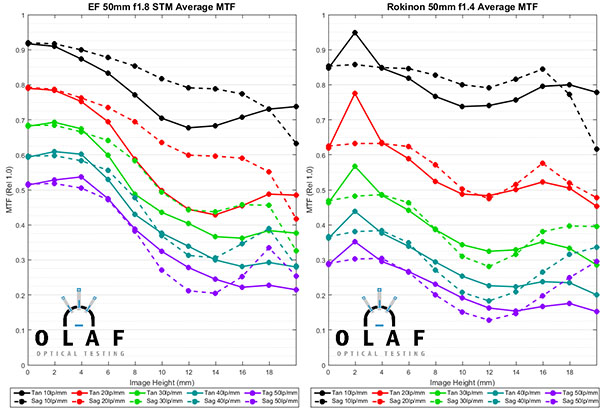
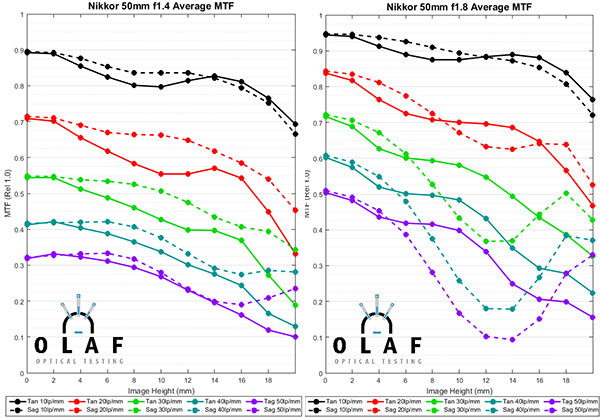
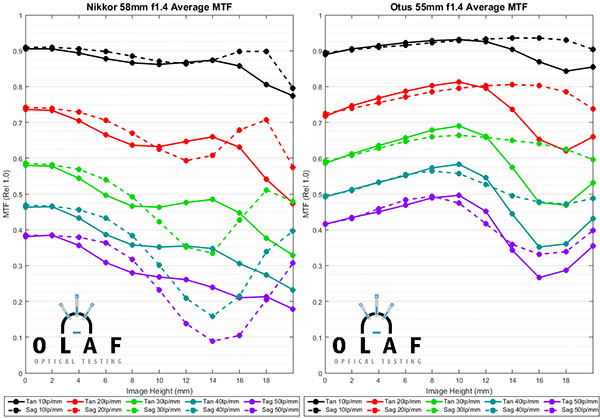
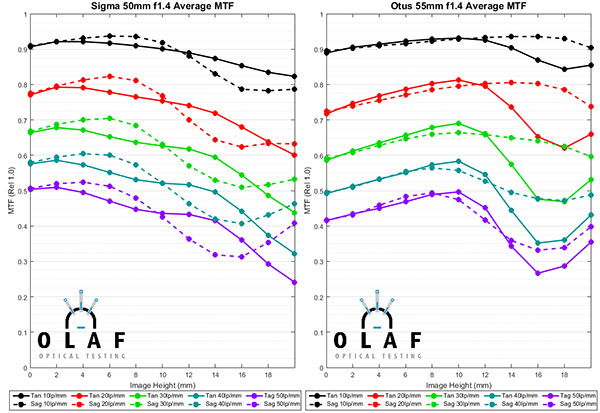
Let’s take a look at the MTF curves for the 50mm lenses. Below are the average curves for each lens. (The Zeiss 55mm f/1.4 Otus graph gets repeated because otherwise one graph would be all sad and lonely, and 562 people would speculate on what my motivation was for singling out whichever one happened to be left alone.) They are in no particular order of anything other than kind of trying to keep lenses of the same brand together.
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015

- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
This article isn’t meant primarily as an MTF comparison but a couple of points are pretty obvious. First, if you can shoot at f/1.8 or f/2.0 you get better resolution. The Zeiss 50mm f/2, and inexpensive Nikon and Canon 50mm f/1.8 have the highest center MTF of any of these lenses. But remember the f/1.4 lenses would have higher MTF if they were stopped down. Nikon shooters might want to take note of the often maligned 58mm f/1.4. When first released, it got beat up pretty savagely for not being as sharp as the Zeiss Otus. It’s not as sharp as the Otus, but it does perform very well.
One note for the MTF gurus among you — you’ll notice an odd spike in the Rokinon 50mm T/1.5 (identified as f/1.4 on the graph above) tangential measurements 2mm off center. This is very consistent in all copies and occurs on both sides from center if we were showing you both sides. We found that the aspheric element causes a localized increase in distortion at that point which mucks with the Optical bench measurements. We could have corrected for it if we had done full distortion mapping of the lens prior to measurement, but time was, as they say, of the essence and it doesn’t affect the big picture. We could hammer that point down to be equal to the sagittal data – where it probably should be – but we don’t believe in fudging the numbers.
Finally, and this is no news to anyone, the Zeiss Otus and the Sigma 50mm f/1.4 Art are more or less tied for resolution champ at 50mm. The Sigma is a bit better near the center, the Otus at the edges, but the differences are small.
For some people the choice of a 50mm lens is made because of its special characteristics; you might absolutely need the aperture of the Canon 50mm f/1.2, the dreamy look of the Zeiss 50mm f/1.4, or the resolution of the Otus. Many more people, though, are looking for just a nice, wide-aperture 50mm prime lens at a reasonable cost. The MTF curves above suggest some of the inexpensive lenses are really quite good. But common wisdom suggests sample variation of those, or of the third-party lenses might be greater than with the more expensive lenses. So we were interested in the copy-to-copy variation among these lenses.
Copy-to-Copy Variation
The simplest way to look at variation is with our Consistency number (for a complete discussion of how we arrive at the Consistency number, see this post). In summary, a higher consistency number means there is less copy-to-copy variation; the lens you buy is more likely to closely resemble the MTF average we presented above. In general, a score over 7 is excellent, a score from 6-7 good, 5-6 okay, 4-5 is a going to have significant copy-to-copy variation, and under 4 is a total crapshoot.
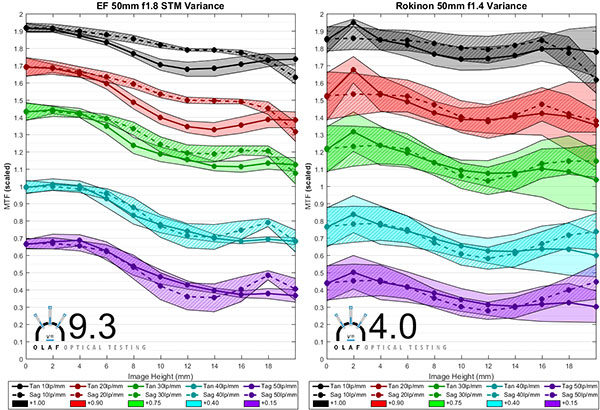
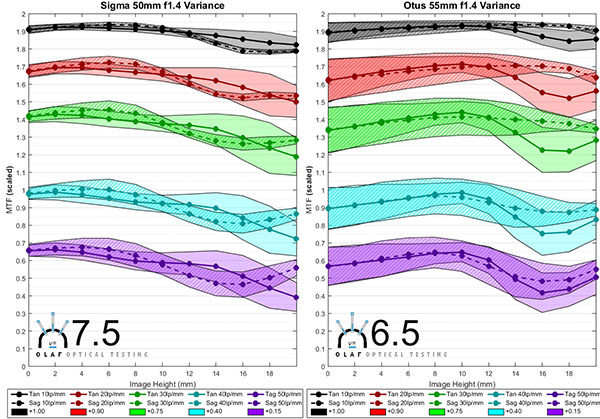
Here are the variation graphs for the 50mm lenses in the same order as we presented the MTFs above. The consistency number is in bold at the lower left of each graph.

- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015

- Roger Cicala and Brandon Dube, Lensrentals.com, 2015

- Roger Cicala and Brandon Dube, Lensrentals.com, 2015

- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
- Roger Cicala and Brandon Dube, Lensrentals.com, 2015
Remember the Consistency number is calculated from the 30 line pairs / mm graph (green one) from center to edge. Looking at the actual graphs gives you more information. For instance some lenses have very little variation in the center and a lot near the edges. That means center sharpness would be very similar in every copy, but corners will be more random. Other lenses vary across the entire field, meaning there might be noticeable differences in center sharpness.
To us, the most surprising finding is that the inexpensive little Canon 50mm f/1.8 STM is incredibly consistent. The Sigma 50mm f/1.4 Art and the Zeiss 50mm f/2 Makro also did exceptionally well, having consistency numbers above 7. Most of the 50mm lenses were above 6, which puts them in what we consider a good range of consistency. The Canon 50mm f/1.4 was a bit behind the pack, but that’s not surprising for an inexpensive 20-year-old design. The Rokinon 50mm f/1.4 had the most variation with a Consistency number of 4, and the Nikon 50mm f/1.4 G was disappointing at 4.6.
We had previously published the Consistency number for 24mm lenses, so I’ll include those in a table for comparison. Wide angle lenses tend to have more variation, so we hoped the 50mm lenses would have less variation than the 24mm lenses.
Lens Consistency
Rokinon 24mm f/1.4 4.0
Nikon 24mm f/1.4 4.6
Sigma 24mm f/1.4 4.9
Canon 24mm f/1.4 Mk II 6.3
Canon 50mm f/1.2 L 6.0
Canon 50mm f/1.4 5.5
Canon 50mm f/1.8 STM 9.3
Nikon 58mm f/1.4 6.7
Nikon 50mm f/1.4 4.6
Nikon 50mm f/1.8 6.3
Zeiss 50mm f/1.4 6.1
Zeiss 50mm f/2 Makro 7.3
Zeiss 55mm f/1.4 Otus 6.5
Sigma 50mm f/1.4 Art 7.5
Rokinon 50mm f/1.4 4.0
Overall, we do see that 50mm lenses tend to have less copy-to-copy variation than 24mm lenses, although it’s not an absolute rule. Canon’s 24mm f/1.4 Mk II has little copy-to-copy variation and scores as well as many of the 50mm lenses. A couple of the 50mm lenses (Rokinon, Nikon, and Canon 50mm f/1.4 lenses) don’t do as well as we hoped.
I think some people expected the Zeiss Otus, given its higher price, to have almost no sample variation. Given the complexity of its design, with more elements in more groups and including a difficult-to-manufacture double-sided aspheric element, it does quite well. The Canon 50mm f/1.8 STM was amazingly consistent, and I’m not sure why. It’s a simple design, but so are several of the other 50mm lenses. I suspect there might be something different in the manufacturing process of this very new lens, but until I take one apart and look inside (we haven’t yet) I’m only speculating.
Trendspotting
We can take a minute to look at a couple of lens variation ‘folk wisdom’ trends to see how they hold up now that we’ve begun testing. First is the idea that wide angle lenses tend to have more variation (lower consistency scores) than longer focal length lenses.

There does seem to be a little bit of truth to that idea, although it’s more at the ‘best end’. No 24mm lens has a consistency score over 6.3, while 5 of the 50mm lenses scored over 6.3. Several of the 50mm lenses had just as much variation as the 24mm lenses.
The next idea is that more expensive lenses have less variation than cheaper lenses. The Canon 50mm f/1.8 STM certainly is the exception to that rule, having the highest consistence score of any lens we’ve published so far and also being the cheapest, but the rest of the lenses do tend to show some correlation that more expensive lenses vary less than less expensive ones. The correlation isn’t as strong as I had hoped, but it’s definitely there.
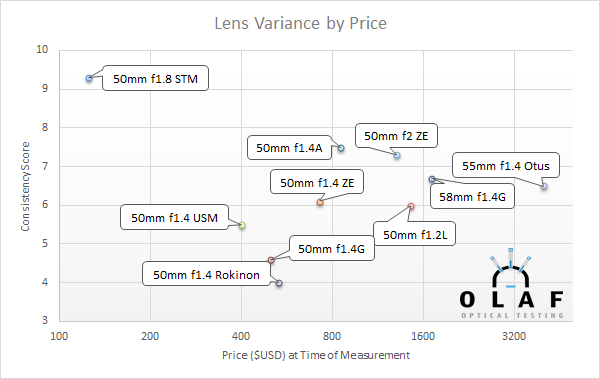
Finally, the 50mm lenses give us a little opportunity to look at year of design. If there’s a pattern here, I can’t clearly see it. But more data points might help, and we’ll be publishing more lenses soon.

Roger Cicala and Brandon Dube
Lensrentals.com
July, 2015
Author: Roger Cicala
I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.
-
Xrqp
-
Madwyn
-
BigEater
-
Doug McEwen
