Lenses and Optics
Some M-Mount Field Curvatures
I haven’t posted very much lately. We’ve had some new equipment installed and we’ve been doing a LOT of testing as we develop our new database of lenses on the optical bench. As the database fills out I’ll be posting more than ever, just because a lot of this stuff is just fun. Today’s post is largely for fun, but will have some additional interest for those who shoot Leica or shoot M-mount lenses adapted to other cameras.
One thing that optical bench testing gives us that is hard to find elsewhere is a clear map of field curvature. We had a client interested in determining field curvatures for a several M-mount lenses and thought there would be a few among you who also wanted to see them.
What These Graphs Are
The graphs are pretty simple: the machine finds the best focus point in the center of the lens (“0” on the vertical axis). It then measures 20 other points from one side to the other of the field, finding the best focus and highest MTF at each point. The relative MTF is shown by color (white>red>orange>yellow, etc.). The focus position compared to best center focus is shown on the vertical axis. The horizontal axis shows position from the left side of an APS-C size sensor to the right.
These lenses were all tested at f/4 to level the playing field for the wider aperture lenses. But this means the field curvature wide open would probably be larger than what you see here. They were done at infinity focus, so the field curvature might be a bit different at shorter focal lengths.
One thing these graphs will show (that you probably don’t really want to know) is that a lot of lenses have a very slight bit of tilt to the field. These are all good copies, tested multiple times. The tilt that is noticeable on these graphs isn’t noticeable in real-world photography, at least not without a great degree of pixel peeping.
The other thing that you may not have thought of is that the sagittal and tangential fields often have different field curvature.
Does this have real-world implications? Yes. The lens with wicked field curvature may give amazingly sharp portraits, but not sharp landscapes or architectural shots, for example. I’m sure someone is going to ask something like, “Well, now many feet does a 100 micron focusing distance equal at infinity?” I don’t have the math to answer that question and don’t have time to go look it all up, but if one of you wants to we’d welcome your input.
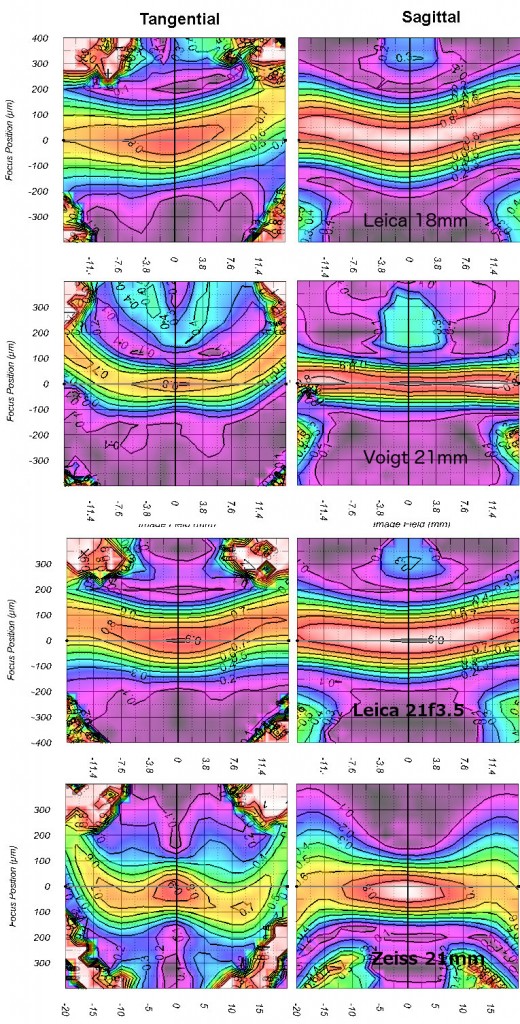
Some wide-angle M-mount lenses.
First we’ll show 4 wide-angle lenses. You may notice the Leica 18mm is very mildly tilted, although this is not something you’d notice in a photograph. The Voigtlander 21mm is a good example of a lens with quite different sagittal and tangential curvatures.
A few that are not quite that wide.
The Leica 28mm f/2.8 gives us a nice example, at least in the sagittal field, of a lens with double (sometimes called Sombrero) curvature.
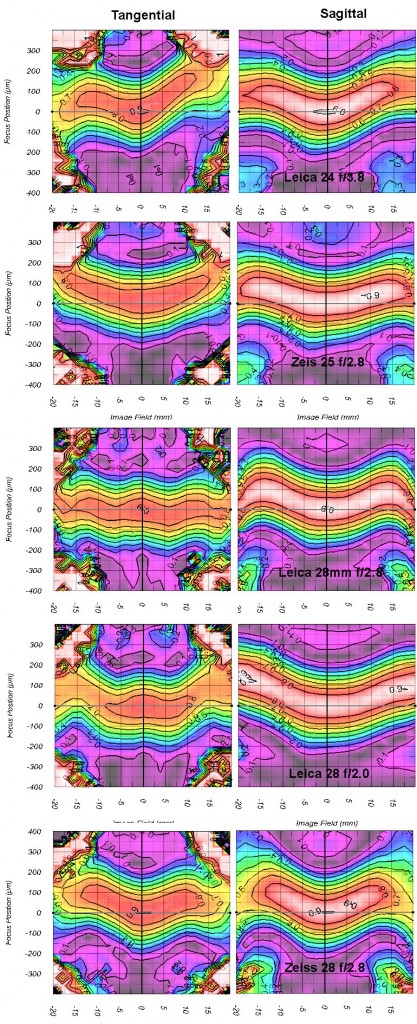
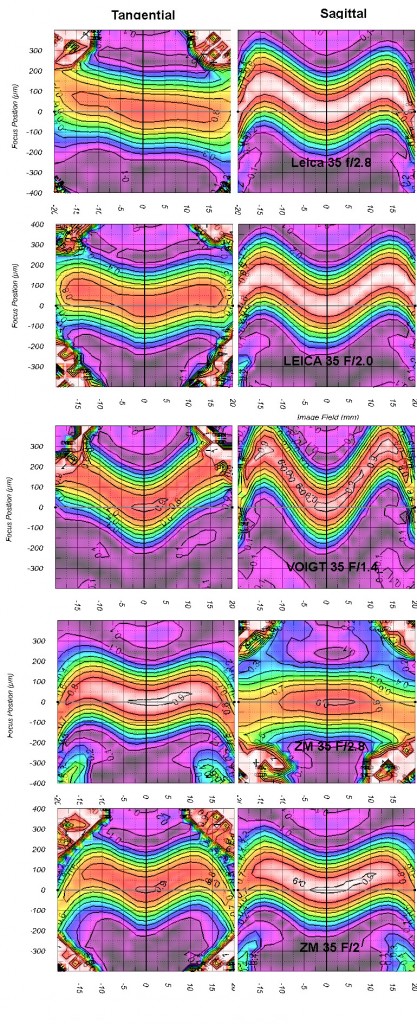
And lastly some 35mm lenses
The Voigtlander 35mm f/1.4 (and remember, this is stopped down to f/4) shows some pretty wicked curvature. Because I know some Voigt fanboy is going to tell me his 35mm has no field curvature I’ll go ahead and tell you that I tested 5 copies and they were all identical. The double field curvature seems to be pretty much standard for these M-mount 35mm lenses.
I don’t have any dramatic conclusions to add, other than I think this is a very useful tool. We’ll be presenting field curvature graphs on all of our lens reports going forward. I’ll also apologize in advance to all of you who want to see the curvature of some specific lens or other. We have over 150 more lenses that need to be tested, minimum of 8 copies of each one, and the zooms at 3 different focal lengths minimum. I’m just not in a position to take requests right now. But we’ll be publishing more of them soon.
Roger Cicala and Aaron Closz
Lensrentals.com
August 2014
Author: Roger Cicala
I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.
-
Curtis Patterson
-
NateW
-
Scott Kirkpatrick
-
Scott Kirkpatrick
-
Mr Will
-
Ilya Zakharevich
-
Ilya Zakharevich
-
David
-
Capablanca
-
Capablanca
-
Samuel H
-
Mike
-
Oskar Ojala
-
grubernd
-
Donald E. Dunbar Jr.
-
Ron
-
Ron
-
Tim Ashley
-
Jose
-
Louis
